pycurve
curves for python
Chandler Armstrong
(omnirizon)
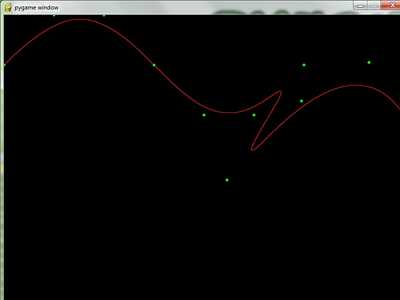
Python implementation of LaGrange, Bezier, and B-spline curves. The algorithms use their respective interpolation/basis functions, so are capable of producing curves of any order. The B-splines use Cox-De Boor and support knot insertion. 2-d only.
see examples, in the download, for a runnable example
To use this library on your own, you will need to know a little bit, but I've done most of the hard work, OK?
This library includes LaGrange, Bezier, and B-spline curves. Lagrange and Bezier are mostly just for educational purposes, what we really want are the B-splines.
B-splines are really just Bezier curves glued together. To make a B-spline you need three things: a set of control points, a vector of knots, and a degree. The control points guide the curve, and the knots direct the curve via these guides. The more knots you have in a curve, the more control you have over how it behaves via the control points. The degree of the curve is actually the order of the comprising Bezier curves (an order 3 Bezier curve is made using three control points). For certain reasons, high order Bezier curves don't behave very well (thus the reason to use B-splines!). This means you should keep the degree low, usually 3 is good enough (in fact, most other B-spline algorithms, including those on this site, just hardcode the algorithms to degree 3, or cubic B-Splines).
There are certain relationships between the number of control points, knots, and the degree, such that if you set two of these numbers, the third must necessary be some value. Look inside my example code for a quick example on how to use these identities to start making B-spline curves. Usually, you will set your control points and degree, and then let the knots be generated automatically as the necessary number of evenly spaced values between 0 and 1 (once again, see the example code). However, this is not necessary, you may want to make your knots not be evenly spaced, in which case you must provide them yourself.
Ok then, just run the demo, inspect that code, and try making your own curves. (no need to worry about diving into the algorithm code, unless you want to learn it, and if you do it is pretty well documented)
Changes
Links
- Home Page
- http://code.google.com/p/pycurve/
Releases
Pygame.org account Comments
-
Frank 2011-07-20 14:18
I think there is a typo on line 96 of _main.py: Shouldn't that 'l' be a '1'? Otherwise nice job!
-
omnirizon 2011-07-23 21:11
indeed. thank you very much.
-
mr 2017-04-03 11:02
Thank you so much, I've been looking for a week for a decent python implementation of these curves that didn't use numpy or scipy. You are a star!