Aesthetic Collisions - 1.0.1

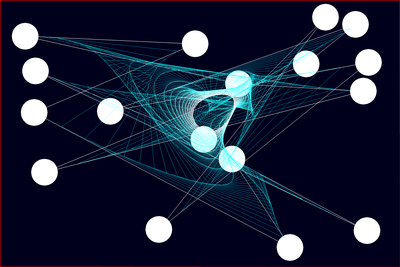
A system of particles colliding is chaotic, so running the exact same code will have drastically different results. This is due to variations in the delay between frames and the usage of floating point numbers as coordinates, as I use a simple collision checker. Rotational momentum is not implemented, and collisions are perfectly elastic. I gave the particles an order and connected them with straight lines to form a polygon from which I recursively drew smaller polygons inscribed in each other to make it look nice. To spice things up, change the settings in `settings.py`: for a start try setting edges=16.

Why this is interesting: Initially, everything is in a predictable, repetitive symmetry. Then, chaos arrives in two waves. The first sign of randomness appears with an unexpected flavour of rotational symmetry. Only after a considerable accumulation of error does the system diffuse into total disorderliness. Here is my explanation for why this occurs: The first of the three stages is simply because of the way it is set up, errors too small to notice. For stage 2, because of the delay between frames, collisions only happen after the intersect a little. Inconsistent delays mean inconsistent variations in angles when a collision occurs, which is why the same initial conditions cause different results. However, floats are precise enough to capture all these little variations. This gives stage 2 its rotational symmetry, since the variations in the delay between frames are the same for each particle in any given execution of code. The final stage simply arrives when the errors accumulated surpasses precision of floats. Ideally, in a symmetrical system, errors should accumulate symmetrically. However, it is not perfectly symmetrical because a particle in the top left corner of the screen would have coordinates [2.307, 2.307] whereas a particle in the bottom right corner would have [717.693, 717.693] implying that the particles at the bottom spend its floats' precision on the integer part of the coordinates, causing asymmetry in errors.