-
pygame.math - pygame module for vector classes
— returns value clamped to min and max. — interpolates between two values by a weight. — a 2-Dimensional Vector — a 3-Dimensional Vector The pygame math module currently provides Vector classes in two and three dimensions,
Vector2andVector3respectively.They support the following numerical operations:
vec + vec,vec - vec,vec * number,number * vec,vec / number,vec // number,vec += vec,vec -= vec,vec *= number,vec /= number,vec //= number,round(vec, ndigits=0).All these operations will be performed elementwise. In addition
vec * vecwill perform a scalar-product (a.k.a. dot-product). If you want to multiply every element from vector v with every element from vector w you can use the elementwise method:v.elementwise() * wThe coordinates of a vector can be retrieved or set using attributes or subscripts
v = pygame.Vector3() v.x = 5 v[1] = 2 * v.x print(v[1]) # 10 v.x == v[0] v.y == v[1] v.z == v[2]
Multiple coordinates can be set using slices or swizzling
v = pygame.Vector2() v.xy = 1, 2 v[:] = 1, 2
New in pygame 1.9.2pre.
Changed in pygame 1.9.4: Removed experimental notice.
Changed in pygame 1.9.4: Allow scalar construction like GLSL Vector2(2) == Vector2(2.0, 2.0)
Changed in pygame 1.9.4:
pygame.mathpygame module for vector classes import not required. More convenientpygame.Vector2andpygame.Vector3.Changed in pygame 2.2.0: round returns a new vector with components rounded to the specified digits.
- pygame.math.clamp()¶
- returns value clamped to min and max.clamp(value, min, max) -> float
Experimental: feature still in development available for testing and feedback. It may change. Please leave clamp feedback with authors
Clamps a numeric
valueso that it's no lower thanmin, and no higher thanmax.New in pygame 2.1.3.
- pygame.math.lerp()¶
- interpolates between two values by a weight.lerp(a, b, weight) -> float
Linearly interpolates between
aandbbyweightusing the formulaa + (b-a) * weight.If
weightis0.5,lerpwill return the value half-way betweenaandb. Whena = 10andb = 20,lerp(a, b, 0.5)will return15. You can think of weight as the percentage of interpolation fromatob,0.0being 0% and1.0being 100%.lerpcan be used for many things. You could rotate a sprite by a weight withangle = lerp(0, 360, weight). You could even scale an enemy's attack value based on the level you're playing:FINAL_LEVEL = 10 current_level = 2 attack = lerp(10, 50, current_level/MAX_LEVEL) # 18
If you're on level 0,
attackwill be10, if you're on level 10,attackwill be50. If you're on level 5, the result ofcurrent_level/MAX_LEVELwill be0.5which represents 50%, thereforeattackwill be30, which is the midpoint of10and50.Raises a ValueError if
weightis outside the range of[0, 1].New in pygame 2.1.3.
- pygame.math.Vector2¶
- a 2-Dimensional VectorVector2() -> Vector2(0, 0)Vector2(int) -> Vector2Vector2(float) -> Vector2Vector2(Vector2) -> Vector2Vector2(x, y) -> Vector2Vector2((x, y)) -> Vector2
— calculates the dot- or scalar-product with the other vector — calculates the cross- or vector-product — returns the Euclidean magnitude of the vector. — returns the squared magnitude of the vector. — returns the Euclidean length of the vector. — returns the squared Euclidean length of the vector. — returns a vector with the same direction but length 1. — normalizes the vector in place so that its length is 1. — tests if the vector is normalized i.e. has length == 1. — scales the vector to a given length. — returns a vector reflected of a given normal. — reflect the vector of a given normal in place. — calculates the Euclidean distance to a given vector. — calculates the squared Euclidean distance to a given vector. — returns a vector moved toward the target by a given distance. — moves the vector toward its target at a given distance. — returns a linear interpolation to the given vector. — returns a spherical interpolation to the given vector. — The next operation will be performed elementwise. — rotates a vector by a given angle in degrees. — rotates a vector by a given angle in radians. — rotates the vector by a given angle in degrees in place. — rotates the vector by a given angle in radians in place. — rotates the vector by a given angle in radians in place. — calculates the angle to a given vector in degrees. — returns a tuple with radial distance and azimuthal angle. — Creates a Vector2(x, y) or sets x and y from a polar coordinates tuple. — projects a vector onto another. — Returns a copy of itself. — Returns a copy of a vector with the magnitude clamped between max_length and min_length. — Clamps the vector's magnitude between max_length and min_length — Sets the coordinates of the vector. — Determines the tolerance of vector calculations. Some general information about the
Vector2class.Changed in pygame 2.1.3: Inherited methods of vector subclasses now correctly return an instance of the subclass instead of the superclass
- dot()¶
- calculates the dot- or scalar-product with the other vectordot(Vector2) -> float
- cross()¶
- calculates the cross- or vector-productcross(Vector2) -> float
calculates the third component of the cross-product.
- magnitude()¶
- returns the Euclidean magnitude of the vector.magnitude() -> float
calculates the magnitude of the vector which follows from the theorem:
vec.magnitude() == math.sqrt(vec.x**2 + vec.y**2)
- magnitude_squared()¶
- returns the squared magnitude of the vector.magnitude_squared() -> float
calculates the magnitude of the vector which follows from the theorem:
vec.magnitude_squared() == vec.x**2 + vec.y**2. This is faster thanvec.magnitude()because it avoids the square root.
- length()¶
- returns the Euclidean length of the vector.length() -> float
calculates the Euclidean length of the vector which follows from the Pythagorean theorem:
vec.length() == math.sqrt(vec.x**2 + vec.y**2)
- length_squared()¶
- returns the squared Euclidean length of the vector.length_squared() -> float
calculates the Euclidean length of the vector which follows from the Pythagorean theorem:
vec.length_squared() == vec.x**2 + vec.y**2. This is faster thanvec.length()because it avoids the square root.
- normalize()¶
- returns a vector with the same direction but length 1.normalize() -> Vector2
Returns a new vector that has
lengthequal to1and the same direction as self.
- normalize_ip()¶
- normalizes the vector in place so that its length is 1.normalize_ip() -> None
Normalizes the vector so that it has
lengthequal to1. The direction of the vector is not changed.
- is_normalized()¶
- tests if the vector is normalized i.e. has length == 1.is_normalized() -> Bool
Returns True if the vector has
lengthequal to1. Otherwise it returnsFalse.
- scale_to_length()¶
- scales the vector to a given length.scale_to_length(float) -> None
Scales the vector so that it has the given length. The direction of the vector is not changed. You can also scale to length
0. If the vector is the zero vector (i.e. has length0thus no direction) aValueErroris raised.
- reflect()¶
- returns a vector reflected of a given normal.reflect(Vector2) -> Vector2
Returns a new vector that points in the direction as if self would bounce of a surface characterized by the given surface normal. The length of the new vector is the same as self's.
- reflect_ip()¶
- reflect the vector of a given normal in place.reflect_ip(Vector2) -> None
Changes the direction of self as if it would have been reflected of a surface with the given surface normal.
- distance_to()¶
- calculates the Euclidean distance to a given vector.distance_to(Vector2) -> float
- distance_squared_to()¶
- calculates the squared Euclidean distance to a given vector.distance_squared_to(Vector2) -> float
- move_towards()¶
- returns a vector moved toward the target by a given distance.move_towards(Vector2, float) -> Vector2
Experimental: feature still in development available for testing and feedback. It may change. Please leave move_towards feedback with authors
Returns a Vector which is moved towards the given Vector by a given distance and does not overshoot past its target Vector. The first parameter determines the target Vector, while the second parameter determines the delta distance. If the distance is in the negatives, then it will move away from the target Vector.
New in pygame 2.1.3.
- move_towards_ip()¶
- moves the vector toward its target at a given distance.move_towards_ip(Vector2, float) -> None
Experimental: feature still in development available for testing and feedback. It may change. Please leave move_towards_ip feedback with authors
Moves itself toward the given Vector at a given distance and does not overshoot past its target Vector. The first parameter determines the target Vector, while the second parameter determines the delta distance. If the distance is in the negatives, then it will move away from the target Vector.
New in pygame 2.1.3.
- lerp()¶
- returns a linear interpolation to the given vector.lerp(Vector2, float) -> Vector2
Returns a Vector which is a linear interpolation between self and the given Vector. The second parameter determines how far between self and other the result is going to be. It must be a value between
0and1where0means self and1means other will be returned.
- slerp()¶
- returns a spherical interpolation to the given vector.slerp(Vector2, float) -> Vector2
Calculates the spherical interpolation from self to the given Vector. The second argument - often called t - must be in the range
[-1, 1]. It parametrizes where - in between the two vectors - the result should be. If a negative value is given the interpolation will not take the complement of the shortest path.
- elementwise()¶
- The next operation will be performed elementwise.elementwise() -> VectorElementwiseProxy
Applies the following operation to each element of the vector.
- rotate()¶
- rotates a vector by a given angle in degrees.rotate(angle) -> Vector2
Returns a vector which has the same length as self but is rotated counterclockwise by the given angle in degrees. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_rad()¶
- rotates a vector by a given angle in radians.rotate_rad(angle) -> Vector2
Returns a vector which has the same length as self but is rotated counterclockwise by the given angle in radians. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.0.0.
- rotate_ip()¶
- rotates the vector by a given angle in degrees in place.rotate_ip(angle) -> None
Rotates the vector counterclockwise by the given angle in degrees. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_ip_rad()¶
- rotates the vector by a given angle in radians in place.rotate_ip_rad(angle) -> None
DEPRECATED: Use rotate_rad_ip() instead.
New in pygame 2.0.0.
Deprecated since pygame 2.1.1.
- rotate_rad_ip()¶
- rotates the vector by a given angle in radians in place.rotate_rad_ip(angle) -> None
Rotates the vector counterclockwise by the given angle in radians. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.1.1.
- angle_to()¶
- calculates the angle to a given vector in degrees.angle_to(Vector2) -> float
Returns the angle from self to the passed
Vector2that would rotate self to be aligned with the passedVector2without crossing over the negative x-axis.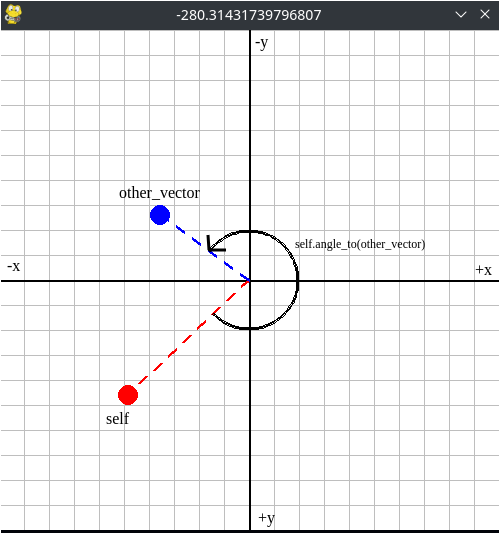
Example demonstrating the angle returned¶
- as_polar()¶
- returns a tuple with radial distance and azimuthal angle.as_polar() -> (r, phi)
Returns a tuple
(r, phi)where r is the radial distance, and phi is the azimuthal angle.
- from_polar()¶
- Creates a Vector2(x, y) or sets x and y from a polar coordinates tuple.Vector2.from_polar((r, phi)) -> Vector2Vector2().from_polar((r, phi)) -> None
If used from the class creates a Vector2(x,y), else sets x and y. The values of x and y are defined from a tuple
(r, phi)where r is the radial distance, and phi is the azimuthal angle.
- project()¶
- projects a vector onto another.project(Vector2) -> Vector2
Returns the projected vector. This is useful for collision detection in finding the components in a certain direction (e.g. in direction of the wall). For a more detailed explanation see Wikipedia.
New in pygame 2.0.2.
- copy()¶
- Returns a copy of itself.copy() -> Vector2
Returns a new Vector2 having the same dimensions.
New in pygame 2.1.1.
- clamp_magnitude()¶
- Returns a copy of a vector with the magnitude clamped between max_length and min_length.clamp_magnitude(max_length) -> Vector2clamp_magnitude(min_length, max_length) -> Vector2
Experimental: feature still in development available for testing and feedback. It may change. Please leave clamp_magnitude feedback with authors
Returns a new copy of a vector with the magnitude clamped between
max_lengthandmin_length. If only one argument is passed, it is taken to be themax_lengthThis function raises
ValueErrorifmin_lengthis greater thanmax_length, or if either of these values are negative.New in pygame 2.1.3.
- clamp_magnitude_ip()¶
- Clamps the vector's magnitude between max_length and min_lengthclamp_magnitude_ip(max_length) -> Noneclamp_magnitude_ip(min_length, max_length) -> None
Experimental: feature still in development available for testing and feedback. It may change. Please leave clamp_magnitude_ip feedback with authors
Clamps the vector's magnitude between
max_lengthandmin_length. If only one argument is passed, it is taken to be themax_lengthThis function raises
ValueErrorifmin_lengthis greater thanmax_length, or if either of these values are negative.New in pygame 2.1.3.
- update()¶
- Sets the coordinates of the vector.update() -> Noneupdate(int) -> Noneupdate(float) -> Noneupdate(Vector2) -> Noneupdate(x, y) -> Noneupdate((x, y)) -> None
Sets coordinates x and y in place.
New in pygame 1.9.5.
- epsilon¶
- Determines the tolerance of vector calculations.
Both Vector classes have a value named
epsilonthat defaults to1e-6. This value acts as a numerical margin in various methods to account for floating point arithmetic errors. Specifically,epsilonis used in the following places:comparing Vectors (
==and!=)the
is_normalizedmethod (if the square of the length is withinepsilonof 1, it's normalized)slerping (a Vector with a length of
<epsilonis considered a zero vector, and can't slerp with that)reflection (can't reflect over the zero vector)
projection (can't project onto the zero vector)
rotation (only used when rotating by a multiple of 90 degrees)
While it's possible to change
epsilonfor a specific instance of a Vector, all the other Vectors will retain the default value. Changingepsilonon a specific instance however could lead to some asymmetric behavior where symmetry would be expected, such asu = pygame.Vector2(0, 1) v = pygame.Vector2(0, 1.2) u.epsilon = 0.5 # don't set it nearly this large print(u == v) # >> True print(v == u) # >> False
You'll probably never have to change
epsilonfrom the default value, but in rare situations you might find that either the margin is too large or too small, in which case changingepsilonslightly might help you out.
- pygame.math.Vector3¶
- a 3-Dimensional VectorVector3() -> Vector3(0, 0, 0)Vector3(int) -> Vector3Vector3(float) -> Vector3Vector3(Vector3) -> Vector3Vector3(x, y, z) -> Vector3Vector3((x, y, z)) -> Vector3
— calculates the dot- or scalar-product with the other vector — calculates the cross- or vector-product — returns the Euclidean magnitude of the vector. — returns the squared Euclidean magnitude of the vector. — returns the Euclidean length of the vector. — returns the squared Euclidean length of the vector. — returns a vector with the same direction but length 1. — normalizes the vector in place so that its length is 1. — tests if the vector is normalized i.e. has length == 1. — scales the vector to a given length. — returns a vector reflected of a given normal. — reflect the vector of a given normal in place. — calculates the Euclidean distance to a given vector. — calculates the squared Euclidean distance to a given vector. — returns a vector moved toward the target by a given distance. — moves the vector toward its target at a given distance. — returns a linear interpolation to the given vector. — returns a spherical interpolation to the given vector. — The next operation will be performed elementwise. — rotates a vector by a given angle in degrees. — rotates a vector by a given angle in radians. — rotates the vector by a given angle in degrees in place. — rotates the vector by a given angle in radians in place. — rotates the vector by a given angle in radians in place. — rotates a vector around the x-axis by the angle in degrees. — rotates a vector around the x-axis by the angle in radians. — rotates the vector around the x-axis by the angle in degrees in place. — rotates the vector around the x-axis by the angle in radians in place. — rotates the vector around the x-axis by the angle in radians in place. — rotates a vector around the y-axis by the angle in degrees. — rotates a vector around the y-axis by the angle in radians. — rotates the vector around the y-axis by the angle in degrees in place. — rotates the vector around the y-axis by the angle in radians in place. — rotates the vector around the y-axis by the angle in radians in place. — rotates a vector around the z-axis by the angle in degrees. — rotates a vector around the z-axis by the angle in radians. — rotates the vector around the z-axis by the angle in degrees in place. — rotates the vector around the z-axis by the angle in radians in place. — rotates the vector around the z-axis by the angle in radians in place. — calculates the angle to a given vector in degrees. — returns a tuple with radial distance, inclination and azimuthal angle. — Creates a Vector3(x, y, z) or sets x, y and z from a spherical coordinates 3-tuple. — projects a vector onto another. — Returns a copy of itself. — Returns a copy of a vector with the magnitude clamped between max_length and min_length. — Clamps the vector's magnitude between max_length and min_length — Sets the coordinates of the vector. — Determines the tolerance of vector calculations. Some general information about the Vector3 class.
Changed in pygame 2.1.3: Inherited methods of vector subclasses now correctly return an instance of the subclass instead of the superclass
- dot()¶
- calculates the dot- or scalar-product with the other vectordot(Vector3) -> float
- cross()¶
- calculates the cross- or vector-productcross(Vector3) -> Vector3
calculates the cross-product.
- magnitude()¶
- returns the Euclidean magnitude of the vector.magnitude() -> float
calculates the magnitude of the vector which follows from the theorem:
vec.magnitude() == math.sqrt(vec.x**2 + vec.y**2 + vec.z**2)
- magnitude_squared()¶
- returns the squared Euclidean magnitude of the vector.magnitude_squared() -> float
calculates the magnitude of the vector which follows from the theorem:
vec.magnitude_squared() == vec.x**2 + vec.y**2 + vec.z**2. This is faster thanvec.magnitude()because it avoids the square root.
- length()¶
- returns the Euclidean length of the vector.length() -> float
calculates the Euclidean length of the vector which follows from the Pythagorean theorem:
vec.length() == math.sqrt(vec.x**2 + vec.y**2 + vec.z**2)
- length_squared()¶
- returns the squared Euclidean length of the vector.length_squared() -> float
calculates the Euclidean length of the vector which follows from the Pythagorean theorem:
vec.length_squared() == vec.x**2 + vec.y**2 + vec.z**2. This is faster thanvec.length()because it avoids the square root.
- normalize()¶
- returns a vector with the same direction but length 1.normalize() -> Vector3
Returns a new vector that has
lengthequal to1and the same direction as self.
- normalize_ip()¶
- normalizes the vector in place so that its length is 1.normalize_ip() -> None
Normalizes the vector so that it has
lengthequal to1. The direction of the vector is not changed.
- is_normalized()¶
- tests if the vector is normalized i.e. has length == 1.is_normalized() -> Bool
Returns True if the vector has
lengthequal to1. Otherwise it returnsFalse.
- scale_to_length()¶
- scales the vector to a given length.scale_to_length(float) -> None
Scales the vector so that it has the given length. The direction of the vector is not changed. You can also scale to length
0. If the vector is the zero vector (i.e. has length0thus no direction) aValueErroris raised.
- reflect()¶
- returns a vector reflected of a given normal.reflect(Vector3) -> Vector3
Returns a new vector that points in the direction as if self would bounce of a surface characterized by the given surface normal. The length of the new vector is the same as self's.
- reflect_ip()¶
- reflect the vector of a given normal in place.reflect_ip(Vector3) -> None
Changes the direction of self as if it would have been reflected of a surface with the given surface normal.
- distance_to()¶
- calculates the Euclidean distance to a given vector.distance_to(Vector3) -> float
- distance_squared_to()¶
- calculates the squared Euclidean distance to a given vector.distance_squared_to(Vector3) -> float
- move_towards()¶
- returns a vector moved toward the target by a given distance.move_towards(Vector3, float) -> Vector3
Experimental: feature still in development available for testing and feedback. It may change. Please leave move_towards feedback with authors
Returns a Vector which is moved towards the given Vector by a given distance and does not overshoot past its target Vector. The first parameter determines the target Vector, while the second parameter determines the delta distance. If the distance is in the negatives, then it will move away from the target Vector.
New in pygame 2.1.3.
- move_towards_ip()¶
- moves the vector toward its target at a given distance.move_towards_ip(Vector3, float) -> None
Experimental: feature still in development available for testing and feedback. It may change. Please leave move_towards_ip feedback with authors
Moves itself toward the given Vector at a given distance and does not overshoot past its target Vector. The first parameter determines the target Vector, while the second parameter determines the delta distance. If the distance is in the negatives, then it will move away from the target Vector.
New in pygame 2.1.3.
- lerp()¶
- returns a linear interpolation to the given vector.lerp(Vector3, float) -> Vector3
Returns a Vector which is a linear interpolation between self and the given Vector. The second parameter determines how far between self an other the result is going to be. It must be a value between
0and1, where0means self and1means other will be returned.
- slerp()¶
- returns a spherical interpolation to the given vector.slerp(Vector3, float) -> Vector3
Calculates the spherical interpolation from self to the given Vector. The second argument - often called t - must be in the range
[-1, 1]. It parametrizes where - in between the two vectors - the result should be. If a negative value is given the interpolation will not take the complement of the shortest path.
- elementwise()¶
- The next operation will be performed elementwise.elementwise() -> VectorElementwiseProxy
Applies the following operation to each element of the vector.
- rotate()¶
- rotates a vector by a given angle in degrees.rotate(angle, Vector3) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise by the given angle in degrees around the given axis. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_rad()¶
- rotates a vector by a given angle in radians.rotate_rad(angle, Vector3) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise by the given angle in radians around the given axis. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.0.0.
- rotate_ip()¶
- rotates the vector by a given angle in degrees in place.rotate_ip(angle, Vector3) -> None
Rotates the vector counterclockwise around the given axis by the given angle in degrees. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_ip_rad()¶
- rotates the vector by a given angle in radians in place.rotate_ip_rad(angle, Vector3) -> None
DEPRECATED: Use rotate_rad_ip() instead.
New in pygame 2.0.0.
Deprecated since pygame 2.1.1.
- rotate_rad_ip()¶
- rotates the vector by a given angle in radians in place.rotate_rad_ip(angle, Vector3) -> None
Rotates the vector counterclockwise around the given axis by the given angle in radians. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.1.1.
- rotate_x()¶
- rotates a vector around the x-axis by the angle in degrees.rotate_x(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the x-axis by the given angle in degrees. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_x_rad()¶
- rotates a vector around the x-axis by the angle in radians.rotate_x_rad(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the x-axis by the given angle in radians. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.0.0.
- rotate_x_ip()¶
- rotates the vector around the x-axis by the angle in degrees in place.rotate_x_ip(angle) -> None
Rotates the vector counterclockwise around the x-axis by the given angle in degrees. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_x_ip_rad()¶
- rotates the vector around the x-axis by the angle in radians in place.rotate_x_ip_rad(angle) -> None
DEPRECATED: Use rotate_x_rad_ip() instead.
New in pygame 2.0.0.
Deprecated since pygame 2.1.1.
- rotate_x_rad_ip()¶
- rotates the vector around the x-axis by the angle in radians in place.rotate_x_rad_ip(angle) -> None
Rotates the vector counterclockwise around the x-axis by the given angle in radians. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.1.1.
- rotate_y()¶
- rotates a vector around the y-axis by the angle in degrees.rotate_y(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the y-axis by the given angle in degrees. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_y_rad()¶
- rotates a vector around the y-axis by the angle in radians.rotate_y_rad(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the y-axis by the given angle in radians. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.0.0.
- rotate_y_ip()¶
- rotates the vector around the y-axis by the angle in degrees in place.rotate_y_ip(angle) -> None
Rotates the vector counterclockwise around the y-axis by the given angle in degrees. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_y_ip_rad()¶
- rotates the vector around the y-axis by the angle in radians in place.rotate_y_ip_rad(angle) -> None
DEPRECATED: Use rotate_y_rad_ip() instead.
New in pygame 2.0.0.
Deprecated since pygame 2.1.1.
- rotate_y_rad_ip()¶
- rotates the vector around the y-axis by the angle in radians in place.rotate_y_rad_ip(angle) -> None
Rotates the vector counterclockwise around the y-axis by the given angle in radians. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.1.1.
- rotate_z()¶
- rotates a vector around the z-axis by the angle in degrees.rotate_z(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the z-axis by the given angle in degrees. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_z_rad()¶
- rotates a vector around the z-axis by the angle in radians.rotate_z_rad(angle) -> Vector3
Returns a vector which has the same length as self but is rotated counterclockwise around the z-axis by the given angle in radians. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.0.0.
- rotate_z_ip()¶
- rotates the vector around the z-axis by the angle in degrees in place.rotate_z_ip(angle) -> None
Rotates the vector counterclockwise around the z-axis by the given angle in degrees. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
- rotate_z_ip_rad()¶
- rotates the vector around the z-axis by the angle in radians in place.rotate_z_ip_rad(angle) -> None
DEPRECATED: Use rotate_z_rad_ip() instead.
Deprecated since pygame 2.1.1.
- rotate_z_rad_ip()¶
- rotates the vector around the z-axis by the angle in radians in place.rotate_z_rad_ip(angle) -> None
Rotates the vector counterclockwise around the z-axis by the given angle in radians. The length of the vector is not changed. (Note that due to pygame's inverted y coordinate system, the rotation will look clockwise if displayed).
New in pygame 2.1.1.
- angle_to()¶
- calculates the angle to a given vector in degrees.angle_to(Vector3) -> float
Returns the angle between self and the given vector.
- as_spherical()¶
- returns a tuple with radial distance, inclination and azimuthal angle.as_spherical() -> (r, theta, phi)
Returns a tuple
(r, theta, phi)where r is the radial distance, theta is the inclination angle and phi is the azimuthal angle.
- from_spherical()¶
- Creates a Vector3(x, y, z) or sets x, y and z from a spherical coordinates 3-tuple.Vector3.from_spherical((r, theta, phi)) -> Vector3Vector3().from_spherical((r, theta, phi)) -> None
If used from the class creates a Vector3(x, y, z), else sets x, y, and z. The values of x, y, and z are from a tuple
(r, theta, phi)where r is the radial distance, theta is the inclination angle and phi is the azimuthal angle.
- project()¶
- projects a vector onto another.project(Vector3) -> Vector3
Returns the projected vector. This is useful for collision detection in finding the components in a certain direction (e.g. in direction of the wall). For a more detailed explanation see Wikipedia.
New in pygame 2.0.2.
- copy()¶
- Returns a copy of itself.copy() -> Vector3
Returns a new Vector3 having the same dimensions.
New in pygame 2.1.1.
- clamp_magnitude()¶
- Returns a copy of a vector with the magnitude clamped between max_length and min_length.clamp_magnitude(max_length) -> Vector3clamp_magnitude(min_length, max_length) -> Vector3
Experimental: feature still in development available for testing and feedback. It may change. Please leave clamp_magnitude feedback with authors
Returns a new copy of a vector with the magnitude clamped between
max_lengthandmin_length. If only one argument is passed, it is taken to be themax_lengthThis function raises
ValueErrorifmin_lengthis greater thanmax_length, or if either of these values are negative.New in pygame 2.1.3.
- clamp_magnitude_ip()¶
- Clamps the vector's magnitude between max_length and min_lengthclamp_magnitude_ip(max_length) -> Noneclamp_magnitude_ip(min_length, max_length) -> None
Experimental: feature still in development available for testing and feedback. It may change. Please leave clamp_magnitude_ip feedback with authors
Clamps the vector's magnitude between
max_lengthandmin_length. If only one argument is passed, it is taken to be themax_lengthThis function raises
ValueErrorifmin_lengthis greater thanmax_length, or if either of these values are negative.New in pygame 2.1.3.
- update()¶
- Sets the coordinates of the vector.update() -> Noneupdate(int) -> Noneupdate(float) -> Noneupdate(Vector3) -> Noneupdate(x, y, z) -> Noneupdate((x, y, z)) -> None
Sets coordinates x, y, and z in place.
New in pygame 1.9.5.
- epsilon¶
- Determines the tolerance of vector calculations.
With lengths within this number, vectors are considered equal. For more information see
pygame.math.Vector2.epsilonDetermines the tolerance of vector calculations.
Edit on GitHub
